Preface ..................................................... ix
1 Background ................................................... 1
1.1 Functional analysis ..................................... 1
1.1.1 Weak topology .................................... 1
1.1.2 Hahn-Banach theorem .............................. 3
1.1.3 Stone-Weierstrass theorem ........................ 4
1.1.4 Banach-Steinhaus theorem ......................... 5
1.1.5 Complex measures ................................. 6
1.1.6 Riesz representation theorem .................... 11
1.1.7 Geometry of Banach spaces ....................... 13
1.2 Operator theory ........................................ 14
1.2.1 Basic definitions and spectral properties ....... 14
1.2.2 Wold decomposition of an isometry ............... 20
1.2.3 Riesz-Dunford functional calculus ............... 21
1.3 The Poisson kernel ..................................... 22
1.4 Hardy spaces ........................................... 23
1.4.1 Inner and outer functions ....................... 25
1.4.2 Consequences of the inner-outer factorization ... 28
1.4.3 The theorems of Beurling and Wiener ............. 30
1.4.4 The disc algebra ................................ 31
1.4.5 Reproducing kernels, Riesz bases and Carleson
sequences ....................................... 31
1.4.6 Functions of bounded mean oscillation ........... 34
1.4.7 The Hilbert transform on the unit circle ........ 35
1.5 Number Theory .......................................... 35
2 The operator-valued Poisson kernel and its applications ..... 37
2.1 The operator-valued Poisson kernel ..................... 37
2.2 The H∞ functional calculus for absolutely continuous
ρ-contractions ......................................... 43
2.3 H∞ functional calculus in a complex Banach space ....... 46
2.4 Absolutely continuous elementary spectral measures ..... 50
Exercises ................................................... 53
Comments .................................................... 54
3 Properties (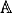 n,m) and factorization of integrable
functions ................................................... 57
3.1 The basis of the S. Brown method ....................... 57
3.1.1 The starting point .............................. 57
3.1.2 The class n,m) and factorization of integrable
functions ................................................... 57
3.1 The basis of the S. Brown method ....................... 57
3.1.1 The starting point .............................. 57
3.1.2 The class 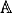 ..................................... 62
3.1.3 Classes ..................................... 62
3.1.3 Classes 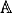 n,m .................................... 63
3.2 Factorization of log-integrable functions .............. 67
3.3 Applications in harmonic analysis ...................... 81
3.4 Subnormal operators .................................... 86
3.4.1 Borelian functional calculus for normal
operators ....................................... 86
3.4.2 Invariant subspaces for subnormal operators ..... 87
3.5 Surjectivity of continuous bilinear mapping ............ 92
3.5.1 A sufficient condition for property ( n,m .................................... 63
3.2 Factorization of log-integrable functions .............. 67
3.3 Applications in harmonic analysis ...................... 81
3.4 Subnormal operators .................................... 86
3.4.1 Borelian functional calculus for normal
operators ....................................... 86
3.4.2 Invariant subspaces for subnormal operators ..... 87
3.5 Surjectivity of continuous bilinear mapping ............ 92
3.5.1 A sufficient condition for property (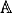  0) ....... 92
3.5.2 A sufficient condition for property ( 0) ....... 92
3.5.2 A sufficient condition for property ( 1, 1, 0) ..... 96
Exercises ................................................... 99
Comments ................................................... 100
4 Polynomially bounded operators with rich spectrum .......... 103
4.1 Apostol's theorem ..................................... 103
4.2 C2( 0) ..... 96
Exercises ................................................... 99
Comments ................................................... 100
4 Polynomially bounded operators with rich spectrum .......... 103
4.1 Apostol's theorem ..................................... 103
4.2 C2( ) functional calculus and the Colojoară-Foias,
theorem ............................................... 107
4.2.1 Operators with a C2( ) functional calculus and the Colojoară-Foias,
theorem ............................................... 107
4.2.1 Operators with a C2( ) functional calculus ..... 107
4.2.2 The Colojoară-Foiaş, theorem ................... 110
4.3 Zenger's theorem ...................................... 111
4.3.1 Zenger's theorem and a factorization result .... 112
4.3.2 A stronger version of Zenger's theorem ......... 114
4.4 Carleson's interpolation theorem ...................... 118
4.5 Approximation using Apostol sets ...................... 123
4.5.1 Approximation of integrable non-negative
functions ...................................... 123
4.5.2 Approximate eigenvalues ........................ 128
4.6 Invariant subspace results ............................ 129
Exercises ............................................ 137
Comments .............................................. 138
5 Beurling algebras .......................................... 141
5.1 Properties of Beurling algebras ....................... 142
5.2 Theorems of Wermer and Atzmon ......................... 146
5.3 Bishop operators ...................................... 152
5.3.1 Davie's functional calculus .................... 152
5.3.2 The point spectrum ............................. 156
5.4 Rational Bishop operators ............................. 160
5.4.1 Cyclic vectors ................................. 161
5.4.2 The lattice of invariant subspaces ............. 163
Exercises .................................................. 167
Comments ................................................... 167
6 Applications of a fixed-point theorem ...................... 169
6.1 Operators commuting with compact operators ............ 169
6.2 Essentially self-adjoint operators .................... 171
6.2.1 Preliminaries .................................. 171
6.2.2 Application to invariant subspaces ............. 177
Exercises ................................................... 180
Comments .................................................... 181
7 Minimal vectors ............................................ 183
7.1 The basic definitions ................................. 183
7.2 Minimal vectors in Hilbert space ...................... 185
7.3 A general extremal problem ........................... 186
7.3.1 Approximation in Hilbert spaces ................ 187
7.3.2 Approximation in reflexive Banach spaces ....... 189
7.4 Application to hyperinvariant subspaces ............... 192
7.4.1 The main theorem ............................... 192
7.4.2 Compact operators .............................. 195
7.4.3 Weighted composition operators ................. 196
7.4.4 Weighted shifts ................................ 205
7.4.5 Multiplication operators on Lp spaces .......... 208
Exercises .................................................. 211
Comments ................................................... 211
8 Universal operators ........................................ 213
8.1 Construction of universal models ...................... 213
8.2 Bilateral weighted shifts ............................. 217
8.3 Composition operators ................................. 220
8.3.1 Universality of composition operators .......... 220
8.3.2 Minimal subspaces and eigenfunctions ........... 224
Exercises .................................................. 228
Comments ................................................... 230
9 Moment sequences and binomial sums ......................... 233
9.1 Moment sequences ...................................... 233
9.2 Operators on sequence spaces .......................... 239
9.3 Binomial sums ......................................... 241
9.3.1 Proof of Theorem 9.3.1 ......................... 242
9.3.2 A technical refinement ......................... 244
9.3.3 Application to Banach algebras and invariant
subspaces ...................................... 248
Exercises .................................................. 251
Comments ................................................... 252
10 Positive and strictly-singular operators ................... 255
10.1 Ordered spaces and positive operators ................. 255
10.2 Invariant subspaces for positive operators ............ 257
10.3 Strictly singular operators ........................... 263
Exercises .................................................. 265
Comments ................................................... 266
References ................................................. 269
Index ...................................................... 281 ) functional calculus ..... 107
4.2.2 The Colojoară-Foiaş, theorem ................... 110
4.3 Zenger's theorem ...................................... 111
4.3.1 Zenger's theorem and a factorization result .... 112
4.3.2 A stronger version of Zenger's theorem ......... 114
4.4 Carleson's interpolation theorem ...................... 118
4.5 Approximation using Apostol sets ...................... 123
4.5.1 Approximation of integrable non-negative
functions ...................................... 123
4.5.2 Approximate eigenvalues ........................ 128
4.6 Invariant subspace results ............................ 129
Exercises ............................................ 137
Comments .............................................. 138
5 Beurling algebras .......................................... 141
5.1 Properties of Beurling algebras ....................... 142
5.2 Theorems of Wermer and Atzmon ......................... 146
5.3 Bishop operators ...................................... 152
5.3.1 Davie's functional calculus .................... 152
5.3.2 The point spectrum ............................. 156
5.4 Rational Bishop operators ............................. 160
5.4.1 Cyclic vectors ................................. 161
5.4.2 The lattice of invariant subspaces ............. 163
Exercises .................................................. 167
Comments ................................................... 167
6 Applications of a fixed-point theorem ...................... 169
6.1 Operators commuting with compact operators ............ 169
6.2 Essentially self-adjoint operators .................... 171
6.2.1 Preliminaries .................................. 171
6.2.2 Application to invariant subspaces ............. 177
Exercises ................................................... 180
Comments .................................................... 181
7 Minimal vectors ............................................ 183
7.1 The basic definitions ................................. 183
7.2 Minimal vectors in Hilbert space ...................... 185
7.3 A general extremal problem ........................... 186
7.3.1 Approximation in Hilbert spaces ................ 187
7.3.2 Approximation in reflexive Banach spaces ....... 189
7.4 Application to hyperinvariant subspaces ............... 192
7.4.1 The main theorem ............................... 192
7.4.2 Compact operators .............................. 195
7.4.3 Weighted composition operators ................. 196
7.4.4 Weighted shifts ................................ 205
7.4.5 Multiplication operators on Lp spaces .......... 208
Exercises .................................................. 211
Comments ................................................... 211
8 Universal operators ........................................ 213
8.1 Construction of universal models ...................... 213
8.2 Bilateral weighted shifts ............................. 217
8.3 Composition operators ................................. 220
8.3.1 Universality of composition operators .......... 220
8.3.2 Minimal subspaces and eigenfunctions ........... 224
Exercises .................................................. 228
Comments ................................................... 230
9 Moment sequences and binomial sums ......................... 233
9.1 Moment sequences ...................................... 233
9.2 Operators on sequence spaces .......................... 239
9.3 Binomial sums ......................................... 241
9.3.1 Proof of Theorem 9.3.1 ......................... 242
9.3.2 A technical refinement ......................... 244
9.3.3 Application to Banach algebras and invariant
subspaces ...................................... 248
Exercises .................................................. 251
Comments ................................................... 252
10 Positive and strictly-singular operators ................... 255
10.1 Ordered spaces and positive operators ................. 255
10.2 Invariant subspaces for positive operators ............ 257
10.3 Strictly singular operators ........................... 263
Exercises .................................................. 265
Comments ................................................... 266
References ................................................. 269
Index ...................................................... 281
|