ПРЕДИСЛОВИЕ ..................................................... 7
РАЗДЕЛ 1. Теория абстрактных полугрупп .......................... 9
1.1 Группоиды, полугруппы и идеалы ............................. 9
1.2 Полугруппы и преобразования ............................... 11
1.3 Обратимость, нильпотентность и регулярность ............... 12
1.4 Отношения и гомоморфизмы .................................. 14
1.5 Теория идеалов ............................................ 16
1.6 Свойства отношений Грина .................................. 16
РАЗДЕЛ 2. Суперматрицы и необратимость ......................... 18
2.1 Линейная супералгебра ..................................... 18
2.2 Суперматричная алгебра .................................... 20
2.3 Суперслед и супердетерминант .............................. 21
2.4 Странные супералгебра, след и детерминант ................. 22
2.5 Идеалы (1ǀ1) × (1ǀ1) суперматриц ........................... 24
РАЗДЕЛ 3. Суперматричные полугруппы, идеальное строение и
редукции ....................................................... 25
3.1 Альтернативная редукция суперматриц ...................... 25
3.1.1 Необратимое строение суперматриц ................... 26
3.1.2 Мультипликативные свойства нечетно-редуцированных
суперматриц ........................................ 28
3.1.3 Унификация редуцированных сунерматриц .............. 28
3.1.4 Скаляры, антискаляры, обобщенные модули и сэндвич-
полугруппа редуцированных суперматриц .............. 29
3.1.5 Прямая сумма редуцированных суперматриц ............ 32
3.1.6 Полугруппа множеств редуцированных матриц .......... 33
3.2 Представление полугрупп связок суперматрицами ............. 34
3.2.1 Правые и левые Г-матрицы ........................... 34
3.2.2 Однопараметрические полугруппы редуцированных
суперматриц ........................................ 36
3.3 Непрерывное суперматричное представление нулевых
полугрупп ................................................. 38
3.3.1 Скрученные прямоугольные связки .................... 40
3.3.2 Представления прямоугольных связок ................ 41
3.3.3 Непрерывные представления высших связок ........... 43
3.3.4 Отношение 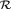 -эквивалентности для прямоугольной
(2ǀ2)-связки ....................................... 45
3.3.5 Топкое идеальное строение высших связок ............ 46
РАЗДЕЛ 4. Необратимое обобщение N = 1 суперконформной
геометрии ...................................................... 51
4.1 Необратимость N = 1 суперконформные преобразования ........ 52
4.1.1 Супераналитические преобразования ................. 52
4.1.2 Касательное суперпространство и варианты его
редукций ........................................... 56
4.1.3 Редуцированные N = 1 преобразования ................ 57
4.1.4 Вырожденные преобразования ......................... 62
4.1.5 Альтернативная параметризация ..................... 64
4.2 N-расширенные суперпространства и необратимые якобианы .... 65
4.2.1. N = 1 суперякобиан ................................. 65
4.3 (1ǀN)-мерное суперпространство ............................ 68
4.3.1. N = 2 березиниан ................................... 70
4.4 Частные случаи редуцированных преобразовании .............. 71
4.5 ρ-суперконформные преобразования и нильпотентные
суперполя ................................................. 71
4.5.1 Полугруппа расщепленных N = 2 SCf преобразований ... 73
4.5.2 Вложение N = 1 → N = 2 ............................. 75
4.6 Суперконформные полугруппы ................................ 76
4.6.1 Локальное строение N = 1 суперконформной
полугруппы ......................................... 76
4.6.2 Ann-полугруппа ..................................... 78
4.6.3 Квазиидеальный ряд ................................. 80
4.6.4 Обобщенные отношения Грина ......................... 81
4.6.5 Квазихарактеры ..................................... 83
4.7 Сплетающие четность преобразования ........................ 84
4.7.1 Касательное суперпространство и кручение четности .. 84
4.7.2 Обобщенное редуцированное расслоение с кручением
четности ........................................... 85
4.7.3 Компонентный анализ ................................ 87
4.8 Нечетные коциклы и деформации ............................. 88
4.8.1 Смешанные условия согласованности и нечетные
аналоги коциклов ................................... 88
4.8.2 Деформации и TPt преобразования .................... 91
4.8.3 Нечетные аналоги препятствий и смешанные θ-
коциклы ............................................ 94
4.9 Нелинейная реализация N = 1 редуцированных
преобразований ............................................ 96
4.9.1 Движение нечетной кривой в -эквивалентности для прямоугольной
(2ǀ2)-связки ....................................... 45
3.3.5 Топкое идеальное строение высших связок ............ 46
РАЗДЕЛ 4. Необратимое обобщение N = 1 суперконформной
геометрии ...................................................... 51
4.1 Необратимость N = 1 суперконформные преобразования ........ 52
4.1.1 Супераналитические преобразования ................. 52
4.1.2 Касательное суперпространство и варианты его
редукций ........................................... 56
4.1.3 Редуцированные N = 1 преобразования ................ 57
4.1.4 Вырожденные преобразования ......................... 62
4.1.5 Альтернативная параметризация ..................... 64
4.2 N-расширенные суперпространства и необратимые якобианы .... 65
4.2.1. N = 1 суперякобиан ................................. 65
4.3 (1ǀN)-мерное суперпространство ............................ 68
4.3.1. N = 2 березиниан ................................... 70
4.4 Частные случаи редуцированных преобразовании .............. 71
4.5 ρ-суперконформные преобразования и нильпотентные
суперполя ................................................. 71
4.5.1 Полугруппа расщепленных N = 2 SCf преобразований ... 73
4.5.2 Вложение N = 1 → N = 2 ............................. 75
4.6 Суперконформные полугруппы ................................ 76
4.6.1 Локальное строение N = 1 суперконформной
полугруппы ......................................... 76
4.6.2 Ann-полугруппа ..................................... 78
4.6.3 Квазиидеальный ряд ................................. 80
4.6.4 Обобщенные отношения Грина ......................... 81
4.6.5 Квазихарактеры ..................................... 83
4.7 Сплетающие четность преобразования ........................ 84
4.7.1 Касательное суперпространство и кручение четности .. 84
4.7.2 Обобщенное редуцированное расслоение с кручением
четности ........................................... 85
4.7.3 Компонентный анализ ................................ 87
4.8 Нечетные коциклы и деформации ............................. 88
4.8.1 Смешанные условия согласованности и нечетные
аналоги коциклов ................................... 88
4.8.2 Деформации и TPt преобразования .................... 91
4.8.3 Нечетные аналоги препятствий и смешанные θ-
коциклы ............................................ 94
4.9 Нелинейная реализация N = 1 редуцированных
преобразований ............................................ 96
4.9.1 Движение нечетной кривой в 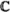 1ǀ1 ................... 96
4.9.2 Глобальная суперсимметрия в 1ǀ1 ................... 96
4.9.2 Глобальная суперсимметрия в 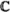 1ǀ1 ................... 96
4.9.3 Редуцированные преобразования ...................... 97
4.9.4 Диаграммный подход к связи между линейной и
нелинейной реализациями ............................ 98
4.9.5 Глобальная двумерная суперсимметрия в терминах
нелинейных реализаций .............................. 98
4.9.6 Нелинейная реализация конечных редуцированных
преобразований .................................... 100
4.10 Дробно-линейные преобразования ........................... 103
4.10.1 Суперконформные преобразования .................... 103
4.10.2 Сплетающие четность преобразования ................ 105
4.10.3 Супераналоги расстояния в 1ǀ1 ................... 96
4.9.3 Редуцированные преобразования ...................... 97
4.9.4 Диаграммный подход к связи между линейной и
нелинейной реализациями ............................ 98
4.9.5 Глобальная двумерная суперсимметрия в терминах
нелинейных реализаций .............................. 98
4.9.6 Нелинейная реализация конечных редуцированных
преобразований .................................... 100
4.10 Дробно-линейные преобразования ........................... 103
4.10.1 Суперконформные преобразования .................... 103
4.10.2 Сплетающие четность преобразования ................ 105
4.10.3 Супераналоги расстояния в 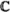 1ǀ1 ................... 105
4.10.4 Необратимый аналог метрики в 1ǀ1 ................... 105
4.10.4 Необратимый аналог метрики в  1ǀ1 ................. 107
РАЗДЕЛ 5. Необратимая геометрия расширенных редуцированных
преобразований ................................................ 108
5.1 N = 2 суперконформная геометрия .......................... 108
5.1.1 Классификация N = 2 расширенных
супераналитических преобразований ................. 109
5.1.2 Компонентное представление и = 2
супераналитическая полугруппа ..................... 110
5.1.3 Редукции N = 2 касательного суперпространства и
перманенты ........................................ 112
5.1.4 Классификация N = 2 SCf преобразований ............ 116
5.1.5 Конечные обратимые и необратимые SCf
преобразования и N = 2 SCf полугруппа ............. 119
5.1.6 Сплетающие четность N = 2 преобразования .......... 124
5.1.7 Дуальные супераналитические N = 1 преобразования
и редуцированные N = 2 преобразования ............. 126
РАЗДЕЛ 6. Перманенты, scf-матрицы и необратимая
гиперболическая геометрия ..................................... 130
6.1 Перманенты и их обобщения для матриц с нильпотентными
элементами ............................................... 130
6.1.1 Перманенты и детерминанты ......................... 130
6.1.2 Полуминоры и полуматрицы .......................... 132
6.2 Свойства scf-матриц и их перманентов ..................... 136
6.2.1 N = 2 scf-матрицы ................................. 136
6.2.2 Ортогональные и scf-матрицы ....................... 138
6.2.3 Обратимость и доопределенные scf-матрицы .......... 139
6.2.4 Полугруппа N = 2 scf-матриц ....................... 140
6.3 Неэвклидова плоскость и scf-матрицы ...................... 141
6.3.1 Определение и свойства реr-отображений ............ 142
6.3.2 Правые и левые двойные отношения .................. 143
6.3.3 Реr-аналог гиперболического расстояния на
суперплоскости .................................... 146
РАЗДЕЛ 7. Теория необратимых супермногообразий ................ 148
7.1 Обратимые супермногообразия и подходы к их описанию ...... 150
7.1.1 Алгебраический подход ............................. 150
7.1.2 Функциональный подход ............................. 151
7.1.3 Различия между алгебраическим и функциональным
подходами ......................................... 152
7.2 Обратимые супермногообразия в терминах окрестностей ...... 153
7.3 Необратимые супермногообразия ............................ 154
7.3.1 Полусупермногообразия ............................. 154
7.3.2 Ориентации полусупермногообразий .................. 157
7.3.3 Препятственность и полумногообразия ............... 157
7.3.4 Полугруппа башенных тождеств ...................... 158
7.3.5 Обобщенная регулярность и полукоммутативные
диаграммы ......................................... 161
7.4 Примеры полусупермногообразий ............................ 163
7.4.1 Модельные супермногообразия ....................... 163
7.4.2 Многозначность и полусупермногообразия ............ 166
7.5 Необратимость и полурасслоения ........................... 168
7.5.1 Определение полурасслоений ........................ 168
7.5.2 Морфизмы полурасслоений ........................... 171
7.6 Необратимость и полугомотопии ............................ 174
СПИСОК ЛИТЕРАТУРЫ ............................................. 177 1ǀ1 ................. 107
РАЗДЕЛ 5. Необратимая геометрия расширенных редуцированных
преобразований ................................................ 108
5.1 N = 2 суперконформная геометрия .......................... 108
5.1.1 Классификация N = 2 расширенных
супераналитических преобразований ................. 109
5.1.2 Компонентное представление и = 2
супераналитическая полугруппа ..................... 110
5.1.3 Редукции N = 2 касательного суперпространства и
перманенты ........................................ 112
5.1.4 Классификация N = 2 SCf преобразований ............ 116
5.1.5 Конечные обратимые и необратимые SCf
преобразования и N = 2 SCf полугруппа ............. 119
5.1.6 Сплетающие четность N = 2 преобразования .......... 124
5.1.7 Дуальные супераналитические N = 1 преобразования
и редуцированные N = 2 преобразования ............. 126
РАЗДЕЛ 6. Перманенты, scf-матрицы и необратимая
гиперболическая геометрия ..................................... 130
6.1 Перманенты и их обобщения для матриц с нильпотентными
элементами ............................................... 130
6.1.1 Перманенты и детерминанты ......................... 130
6.1.2 Полуминоры и полуматрицы .......................... 132
6.2 Свойства scf-матриц и их перманентов ..................... 136
6.2.1 N = 2 scf-матрицы ................................. 136
6.2.2 Ортогональные и scf-матрицы ....................... 138
6.2.3 Обратимость и доопределенные scf-матрицы .......... 139
6.2.4 Полугруппа N = 2 scf-матриц ....................... 140
6.3 Неэвклидова плоскость и scf-матрицы ...................... 141
6.3.1 Определение и свойства реr-отображений ............ 142
6.3.2 Правые и левые двойные отношения .................. 143
6.3.3 Реr-аналог гиперболического расстояния на
суперплоскости .................................... 146
РАЗДЕЛ 7. Теория необратимых супермногообразий ................ 148
7.1 Обратимые супермногообразия и подходы к их описанию ...... 150
7.1.1 Алгебраический подход ............................. 150
7.1.2 Функциональный подход ............................. 151
7.1.3 Различия между алгебраическим и функциональным
подходами ......................................... 152
7.2 Обратимые супермногообразия в терминах окрестностей ...... 153
7.3 Необратимые супермногообразия ............................ 154
7.3.1 Полусупермногообразия ............................. 154
7.3.2 Ориентации полусупермногообразий .................. 157
7.3.3 Препятственность и полумногообразия ............... 157
7.3.4 Полугруппа башенных тождеств ...................... 158
7.3.5 Обобщенная регулярность и полукоммутативные
диаграммы ......................................... 161
7.4 Примеры полусупермногообразий ............................ 163
7.4.1 Модельные супермногообразия ....................... 163
7.4.2 Многозначность и полусупермногообразия ............ 166
7.5 Необратимость и полурасслоения ........................... 168
7.5.1 Определение полурасслоений ........................ 168
7.5.2 Морфизмы полурасслоений ........................... 171
7.6 Необратимость и полугомотопии ............................ 174
СПИСОК ЛИТЕРАТУРЫ ............................................. 177
|