1 Introduction ................................................. 6
2 Integral formulae for the interpolation error term ........... 9
2.1 General formula ......................................... 9
2.1.1 Definitions and historic remarks ................. 9
2.1.2 General theorem ................................. 10
2.1.3 Examples of classes I(T, Z) ..................... 12
2.2 Interpolation formulae for T = 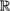 and Z = i and Z = i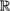 \ {0} ..... 12
2.2.1 Special case .................................... 12
2.2.2 Differentiability and continuity properties ..... 13
2.2.3 Interpolation theorems .......................... 15
2.2.4 Even and odd functions .......................... 17
2.3 Interpolation formulae for functions |y|s(sgn y)l
logν |y| ............................................... 21
2.3.1 General nodes ................................... 21
2.3.2 Symmetric nodes ................................. 25
3 Asymptotic properties of special sequences of polynomials ... 29
3.1 Three classes of special sequences of polynomials ...... 29
3.1.1 Class \ {0} ..... 12
2.2.1 Special case .................................... 12
2.2.2 Differentiability and continuity properties ..... 13
2.2.3 Interpolation theorems .......................... 15
2.2.4 Even and odd functions .......................... 17
2.3 Interpolation formulae for functions |y|s(sgn y)l
logν |y| ............................................... 21
2.3.1 General nodes ................................... 21
2.3.2 Symmetric nodes ................................. 25
3 Asymptotic properties of special sequences of polynomials ... 29
3.1 Three classes of special sequences of polynomials ...... 29
3.1.1 Class  d(β,γ,δ) ................................. 29
3.1.2 Class d(β,γ,δ) ................................. 29
3.1.2 Class  d*(β,γ,δ) ................................ 30
3.1.3 Class d*(β,γ,δ) ................................ 30
3.1.3 Class  d**(β,γ,δ, W, k) ......................... 33
3.2 Examples of sequences from the classes d**(β,γ,δ, W, k) ......................... 33
3.2 Examples of sequences from the classes  d, d,  d*, and d*, and
 d** ................................................... 35
3.2.1 Normalised Gegenbauer polynomials on [-1,1] ..... 35
3.2.2 Normalized Chebyshev polynomials on [-1,1] ...... 36
3.2.3 Normalized polynomials with equidistant zeros
on [-1,1] ....................................... 38
3.2.4 Normalized Hermite polynomials on (-∞, ∞) ....... 41
3.2.5 Normalized Williams-Apostol polynomials on
(-co, oo) ....................................... 43
3.2.6 Normalized Lommel polynomials on (-∞, ∞) ........ 46
3.2.7 Normalized Laguerre polynomials on (-∞, ∞) ...... 47
3.3 Asymptotic formulae for Lp-quasinorms of special
polynomials ............................................ 47
3.3.1 Technical lemma ................................. 47
3.3.2 Normalized Gegenbauer polynomials on [-1,1] ..... 50
3.3.3 Normalized even Chebyshev polynomials of the
first kind on [-1,1] ............................ 54
3.3.4 Normalized polynomials with equidistant zeros
on [-1,1] ....................................... 54
3.3.5 Normalized Hermite polynomials on (-∞, ∞) ....... 55
3.3.6 Normalized Williams-Apostol polynomials on
(-∞, ∞) ......................................... 64
4 Pointwise asymptotic relations between the interpolation
error and zeta functions .................................... 65
4.1 Estimates for integrals ................................ 65
4.2 Asymptotic relations for ζ(s) and β(s) ................. 69
4.3 Some corollaries ....................................... 73
4.4 Asymptotic summation formulae for zeta functions ....... 76
5 Asymptotic relations between the Lp-mterpolation error and
zeta functions .............................................. 85
5.1 Lp-asymptotics for the integral term ................... 85
5.2 Lp-asymptotic representations for zeta functions ....... 90
5.2.1 General theorem ................................. 90
5.2.2 Examples ........................................ 91
5.3 Interpolation L∞-error criteria for ζ0,k(s) ≠ 0
and ζ0,k(s) = 0 ........................................ 98
5.3.1 General L∞-error criterion ...................... 98
5.3.2 Special L∞-error criteria ...................... 100
5.4 Interpolation Lp-error criteria for Ld,k(s) ≠ 0 and
ζ0,k(s) = 0 ............................................ 101
5.4.1 General Lp-error criterion ..................... 101
5.4.2 Special Lp-error criteria ...................... 101
6 Other applications ......................................... 105
6.1 Universal exponential sums ............................ 105
6.2 Functional equations for zeta functions ............... 107
6.3 Combinatorial representations for Bernoulli and
Euler numbers ......................................... 109
References ................................................. 113
Index ......................................................... 116 d** ................................................... 35
3.2.1 Normalised Gegenbauer polynomials on [-1,1] ..... 35
3.2.2 Normalized Chebyshev polynomials on [-1,1] ...... 36
3.2.3 Normalized polynomials with equidistant zeros
on [-1,1] ....................................... 38
3.2.4 Normalized Hermite polynomials on (-∞, ∞) ....... 41
3.2.5 Normalized Williams-Apostol polynomials on
(-co, oo) ....................................... 43
3.2.6 Normalized Lommel polynomials on (-∞, ∞) ........ 46
3.2.7 Normalized Laguerre polynomials on (-∞, ∞) ...... 47
3.3 Asymptotic formulae for Lp-quasinorms of special
polynomials ............................................ 47
3.3.1 Technical lemma ................................. 47
3.3.2 Normalized Gegenbauer polynomials on [-1,1] ..... 50
3.3.3 Normalized even Chebyshev polynomials of the
first kind on [-1,1] ............................ 54
3.3.4 Normalized polynomials with equidistant zeros
on [-1,1] ....................................... 54
3.3.5 Normalized Hermite polynomials on (-∞, ∞) ....... 55
3.3.6 Normalized Williams-Apostol polynomials on
(-∞, ∞) ......................................... 64
4 Pointwise asymptotic relations between the interpolation
error and zeta functions .................................... 65
4.1 Estimates for integrals ................................ 65
4.2 Asymptotic relations for ζ(s) and β(s) ................. 69
4.3 Some corollaries ....................................... 73
4.4 Asymptotic summation formulae for zeta functions ....... 76
5 Asymptotic relations between the Lp-mterpolation error and
zeta functions .............................................. 85
5.1 Lp-asymptotics for the integral term ................... 85
5.2 Lp-asymptotic representations for zeta functions ....... 90
5.2.1 General theorem ................................. 90
5.2.2 Examples ........................................ 91
5.3 Interpolation L∞-error criteria for ζ0,k(s) ≠ 0
and ζ0,k(s) = 0 ........................................ 98
5.3.1 General L∞-error criterion ...................... 98
5.3.2 Special L∞-error criteria ...................... 100
5.4 Interpolation Lp-error criteria for Ld,k(s) ≠ 0 and
ζ0,k(s) = 0 ............................................ 101
5.4.1 General Lp-error criterion ..................... 101
5.4.2 Special Lp-error criteria ...................... 101
6 Other applications ......................................... 105
6.1 Universal exponential sums ............................ 105
6.2 Functional equations for zeta functions ............... 107
6.3 Combinatorial representations for Bernoulli and
Euler numbers ......................................... 109
References ................................................. 113
Index ......................................................... 116
|