Preface ........................................................ ix
About the Authors ............................................ xiii
List of Symbols ................................................ xv
Introduction .................................................... 1
I Preliminaries ............................................... 9
1 Three-Dimensional Euclidean Space 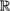 3 ........................ 11
1.1 Basic Notation ......................................... 11
1.2 Integral Theorems ...................................... 22
1.3 Exercises .............................................. 27
2 Two-Dimensional Sphere Ω .................................... 29
2.1 Basic Notation ......................................... 29
2.2 Integral Theorems ...................................... 35
2.3 (Scalar) Spherical Harmonics ........................... 42
2.4 (Scalar) Circular Harmonics ............................ 52
2.5 Vector Spherical Harmonics ............................. 59
2.6 Tensor Spherical Harmonics ............................. 69
2.7 Exercises .............................................. 76
II Potential Theory in the Euclidean Space 3 ........................ 11
1.1 Basic Notation ......................................... 11
1.2 Integral Theorems ...................................... 22
1.3 Exercises .............................................. 27
2 Two-Dimensional Sphere Ω .................................... 29
2.1 Basic Notation ......................................... 29
2.2 Integral Theorems ...................................... 35
2.3 (Scalar) Spherical Harmonics ........................... 42
2.4 (Scalar) Circular Harmonics ............................ 52
2.5 Vector Spherical Harmonics ............................. 59
2.6 Tensor Spherical Harmonics ............................. 69
2.7 Exercises .............................................. 76
II Potential Theory in the Euclidean Space 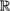 3 ................. 81
3 Basic Concepts .............................................. 83
3.1 Background Material .................................... 83
3.2 Volume Potentials ...................................... 99
3.3 Surface Potentials .................................... 103
3.4 Boundary-Value Problems ............................... 126
3.5 Locally and Globally Uniform Approximation ............ 152
3.6 Exercises ............................................. 171
4 Gravitation ................................................ 175
4.1 Oblique Derivative Problem ............................ 181
4.2 Satellite Problems .................................... 212
4.3 Gravimetry Problem .................................... 224
4.4 Exercises ............................................. 237
5 Geomagnetism ............................................... 243
5.1 Geomagnetic Background ................................ 243
5.2 Mie and Helmholtz Decompositions ...................... 248
5.3 Gauss Representation and Uniqueness ................... 256
5.4 Separation of Sources ................................. 266
5.5 Ionospheric Current Systems ........................... 272
5.6 Exercises ............................................. 283
III Potential Theory on the Unit Sphere Ω .................... 285
6 Basic Concepts ............................................. 287
6.1 Background Material ................................... 287
6.2 Surface Potentials .................................... 293
6.3 Curve Potentials ...................................... 297
6.4 Boundary-Value Problems ............................... 316
6.5 Differential Equations for 3 ................. 81
3 Basic Concepts .............................................. 83
3.1 Background Material .................................... 83
3.2 Volume Potentials ...................................... 99
3.3 Surface Potentials .................................... 103
3.4 Boundary-Value Problems ............................... 126
3.5 Locally and Globally Uniform Approximation ............ 152
3.6 Exercises ............................................. 171
4 Gravitation ................................................ 175
4.1 Oblique Derivative Problem ............................ 181
4.2 Satellite Problems .................................... 212
4.3 Gravimetry Problem .................................... 224
4.4 Exercises ............................................. 237
5 Geomagnetism ............................................... 243
5.1 Geomagnetic Background ................................ 243
5.2 Mie and Helmholtz Decompositions ...................... 248
5.3 Gauss Representation and Uniqueness ................... 256
5.4 Separation of Sources ................................. 266
5.5 Ionospheric Current Systems ........................... 272
5.6 Exercises ............................................. 283
III Potential Theory on the Unit Sphere Ω .................... 285
6 Basic Concepts ............................................. 287
6.1 Background Material ................................... 287
6.2 Surface Potentials .................................... 293
6.3 Curve Potentials ...................................... 297
6.4 Boundary-Value Problems ............................... 316
6.5 Differential Equations for  * and L* .................. 333
6.6 Locally and Globally Uniform Approximation ............ 336
6.7 Exercises ............................................. 342
7 Gravitation ................................................ 347
7.1 Disturbing Potential .................................. 347
7.2 Linear Regularization Method .......................... 359
7.3 Multiscale Solution ................................... 363
7.4 Exercises ............................................. 381
8 Geomagnetism ............................................... 385
8.1 Mie and Helmholtz Decomposition ....................... 385
8.2 Higher-Order Regularization Methods ................... 395
8.3 Separation of Sources ................................. 404
8.4 Ionospheric Current Systems ........................... 411
8.5 Exercises ............................................. 426
Bibliography .................................................. 429
Index ......................................................... 449 * and L* .................. 333
6.6 Locally and Globally Uniform Approximation ............ 336
6.7 Exercises ............................................. 342
7 Gravitation ................................................ 347
7.1 Disturbing Potential .................................. 347
7.2 Linear Regularization Method .......................... 359
7.3 Multiscale Solution ................................... 363
7.4 Exercises ............................................. 381
8 Geomagnetism ............................................... 385
8.1 Mie and Helmholtz Decomposition ....................... 385
8.2 Higher-Order Regularization Methods ................... 395
8.3 Separation of Sources ................................. 404
8.4 Ionospheric Current Systems ........................... 411
8.5 Exercises ............................................. 426
Bibliography .................................................. 429
Index ......................................................... 449
|