Introduction .................................................... 1
Chapter 1 Preliminaries ........................................ 5
Chapter 2 Basic Solutions ...................................... 9
2.1 Properties of basic solutions .............................. 9
2.2 The spectral equation and Spec(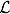 0) ........................ 11
2.3 Existence of basic solutions .............................. 13
2.4 Properties of the fundamental matrix of (Eσ 0) ........................ 11
2.3 Existence of basic solutions .............................. 13
2.4 Properties of the fundamental matrix of (Eσ ) ............. 14
2.5 The system of equations for the adjoint operator ) ............. 14
2.5 The system of equations for the adjoint operator 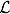  * ...... 16
2.6 Continuation of a simple spectral value ................... 17
2.7 Continuation of a double spectral value ................... 19
2.8 Purely imaginary spectral value ........................... 22
2.9 Main result about basic solutions ......................... 24
Chapter 3 Example ............................................. 27
Chapter 4 Asymptotic behavior of the basic solutions of * ...... 16
2.6 Continuation of a simple spectral value ................... 17
2.7 Continuation of a double spectral value ................... 19
2.8 Purely imaginary spectral value ........................... 22
2.9 Main result about basic solutions ......................... 24
Chapter 3 Example ............................................. 27
Chapter 4 Asymptotic behavior of the basic solutions of 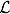 ..... 29
4.1 Estimate of σ ............................................. 30
4.2 First estimate of Φ and ψ ................................. 33
4.3 End of the proof of Theorem 4.1 ........................... 34
Chapter 5 The kernels ......................................... 37
5.1 Two lemmas ................................................ 38
5.2 Proof of Theorem 5.1 ...................................... 40
5.3 Modified kernels .......................................... 41
Chapter 6 The homogeneous equation ..... 29
4.1 Estimate of σ ............................................. 30
4.2 First estimate of Φ and ψ ................................. 33
4.3 End of the proof of Theorem 4.1 ........................... 34
Chapter 5 The kernels ......................................... 37
5.1 Two lemmas ................................................ 38
5.2 Proof of Theorem 5.1 ...................................... 40
5.3 Modified kernels .......................................... 41
Chapter 6 The homogeneous equation 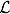 u = 0 ..................... 43
6.1 Representation of solutions in a cylinder ................. 43
6.2 Cauchy integral formula ................................... 46
6.3 Consequences .............................................. 47
Chapter 7 The nonhomogeneous equation u = 0 ..................... 43
6.1 Representation of solutions in a cylinder ................. 43
6.2 Cauchy integral formula ................................... 46
6.3 Consequences .............................................. 47
Chapter 7 The nonhomogeneous equation 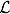 u = F .................. 51
7.1 Generalized Cauchy Integral Formula ....................... 51
7.2 The integral operator T ................................... 52
7.3 Compactness of the operator T ............................. 55
Chapter 8 The semilinear equation ............................. 57
Chapter 9 The second order equation: Reduction ................ 61
Chapter 10 The homogeneous equation Pu = 0 ..................... 63
10.1 Some properties .......................................... 63
10.2 Main result about the homogeneous equation Pu = 0 ........ 65
10.3 A maximum principle ...................................... 67
Chapter 11 The nonhomogeneous equation Pu = F .................. 69
Chapter 12 Normalization of a Class of Second Order Equations
with a Singularity .................................. 73
Bibliography ................................................... 77 u = F .................. 51
7.1 Generalized Cauchy Integral Formula ....................... 51
7.2 The integral operator T ................................... 52
7.3 Compactness of the operator T ............................. 55
Chapter 8 The semilinear equation ............................. 57
Chapter 9 The second order equation: Reduction ................ 61
Chapter 10 The homogeneous equation Pu = 0 ..................... 63
10.1 Some properties .......................................... 63
10.2 Main result about the homogeneous equation Pu = 0 ........ 65
10.3 A maximum principle ...................................... 67
Chapter 11 The nonhomogeneous equation Pu = F .................. 69
Chapter 12 Normalization of a Class of Second Order Equations
with a Singularity .................................. 73
Bibliography ................................................... 77
|