1 Introduction ................................................. 1
2 Segal Г-Spaces ............................................... 9
2.1 Segal Г-Spaces - a Covariant Version .................... 9
2.2 Segal Г-Spaces Arising From Categories ................. 11
2.3 Segal Г-Spaces and Spectra ............................. 12
3 Infinite Symmetric Products and Singular Homology ........... 17
3.1 Definition ............................................. 17
3.2 Dold-Thom Theorem and Dold-Puppe Splitting ............. 19
3.3 Generalized Symmetric Product .......................... 21
3.4 Splitting of SP  n ..................................... 22
3.5 Splitting of SP ...................................... 25
4 Configuration Spaces and Stable Homotopy Theory ............. 27
4.1 Properties of Configurations and Examples .............. 27
4.2 Braid Groups ........................................... 28
4.3 Snaith Splitting and Stable Homotopy Theory ............ 29
4.4 Г-spaces arising from  ( 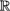 ) ........................... 35
5 Grassmannians and Connective K-Theory ....................... 37
5.1 Connective K-Homology Theory ........................... 37
5.2 The Sheaf of Parameterized Embeddings .................. 41
5.2.1 Topology on the Sheaf Bd(-; Y) .................. 41
5.2.2 Section Space Sectd(M; Y+) ...................... 49
5.2.3 A Scanning Construction for the Thom Spectrum
МТОd ............................................ 50
5.3 Splitting of the Functor К ............................. 55
5.3.1 Homotopy Type of the Splitting Space  (Y+) ...... 55
5.3.2 Proof of the Main Theorem ....................... 57
6 Splitting of Segal Г-Spaces ................................. 65
6.1 Weight Filtration of  (X) ............................. 65
6.2 Duality Theorem ........................................ 67
6.3 Splitting Spaces ....................................... 68
6.4 Splitting of Segal Г-Spaces ............................ 69
6.5 Homotopy Calculus of Segal Г-Spaces .................... 71
Аppendices ..................................................... 74
Gromov's h-principle ........................................ 75
Homotopy Calculus of Functors: an Overview .................. 79
Вibliography ................................................... 83
| 
