Preface ....................................................... vii
CHAPTER 1. Introduction ......................................... 1
1.1 Formulation of the Integer Programming Problem ............. 1
1.2 Reformulation of Integer Programming Problems .............. 4
1.2.1 Transformation to Binary Problems ................... 6
1.2.2 Linearization of the Nonlinear Problems ............. 6
1.2.3 Constraint Aggregation .............................. 7
1.2.4 Optimization Problems in Finite Sets ................ 9
1.3 Basic Relaxations of Integer Programming Problems ......... 10
1.4 The Idea of Integer Programming Methods ................... 12
1.5 Applications of Integer Programming ....................... 13
1.5.1 The Knapsack Problem ............................... 13
1.5.2 The Cutting-Stock Problem .......................... 14
1.5.3 The Capacitated Plant Location Problem ............. 15
1.5.4 The Assignment Problem ............................. 16
1.5.5 The Travelling Salesman Problem .................... 17
1.5.6 The Quadratic Assignment Problem ................... 18
1.5.7 Dichotomies and the Piecewise Linear
Approximation ...................................... 19
1.6 A Brief Introduction to Computational Complexity .......... 20
1.6.1 Complexity of Algorithms ........................... 20
1.6.2 The Classes  and 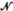 ............................. 21
1.7 Bibliographic Notes ....................................... 23
1.8 Exercises ................................................. 24
CHAPTER 2. Linear Programming .................................. 25
2.1 Basic Solutions ........................................... 25
2.2 The Simplex Method ........................................ 27
2.2.1. Simplex Tableaus ................................... 29
2.3 The First Basic Feasible Solution ......................... 31
2.4 Degenerate Solutions ...................................... 32
2.5 Bounded Variables ......................................... 33
2.6 Duality ................................................... 35
2.7 The Dual Simplex Algorithm ................................ 38
2.8 Remarks about the Efficiency of the Simplex Method ........ 39
2.9 The Ellipsoid Algorithm ................................... 42
2.9.1 The Idea of the Ellipsoid Algorithm ................ 42
2.9.2 The Basic Iteration of the Ellipsoid Algorithm ..... 44
2.9.3 Polynomiality ...................................... 47
2.9.4 Solving the Linear Programming Problems ............ 50
2.10 Subgradient Methods ....................................... 52
2.11 Bibliographic Notes ....................................... 54
2.12 Exercises ................................................. 55
CHAPTER 3. Unimodularity and Network Flows. Cutting-Plane
Methods ............................................. 57
3.1 Integrality of Data ....................................... 57
3.2 Unimodularity ............................................. 60
3.3 Basic Definitions of Graph Theory ......................... 62
3.4 Flows in Networks ......................................... 63
3.4.1 General Formulation ................................ 64
3.4.2 Some Particular Cases .............................. 65
3.4.3 Dijkstra's Method .................................. 67
3.5 A Fundamental Cut ......................................... 68
3.6 Finiteness of the Method of Integer Forms ................. 72
3.7 Other Modifications of the Cutting-Plane Method ........... 73
3.7.1 Dual All-Integer Cuts .............................. 74
3.7.2 Primal All-Integer Cuts ............................ 75
3.7.3 Stronger Cuts ...................................... 75
3.8 Bibliographic Notes ....................................... 76
3.9 Exercises ................................................. 77
CHAPTER 4. Branch-and-Bound Methods ............................ 79
4.1 The Idea of a Branch-and-Bound Method ..................... 79
4.1.1 Terminology ........................................ 80
4.1.2 Remarks about the Efficiency of a Branch-and-
Bound Method ....................................... 82
4.2 Improving Bounds .......................................... 83
4.3 The Choice of a Subproblem ................................ 85
4.4 The Selection of a Branching Variable ..................... 87
4.5 Bibliographic Notes ....................................... 88
4.6 Exercises ................................................. 88
CHAPTER 5. The Knapsack Problem ................................ 90
5.1 Relaxations ............................................... 90
5.1.1 The Linear Programming Relaxation .................. 91
5.1.2 A Linear-Time Algorithm ............................ 92
5.1.3 Lagrangean Relaxations ............................. 94
5.2 Reduction Methods ......................................... 95
5.3 The Branch-and-Bound Approach ............................. 96
5.4 Dynamic Programming ....................................... 97
5.5 The Knapsack Polytope ..................................... 98
5.6 The Multiple-Choice Knapsack Problem ...................... 99
5.6.1 Relaxations of MA ................................. 100
5.6.2 Dominance Relations ............................... 104
5.7 Bibliographic Notes ...................................... 106
5.8 Exercises ................................................ 107
CHAPTER 6. Equivalent Formulations for Integer Programs ....... 109
6.1 The Reduction of the Size of Binary Problems ............. 109
6.2 The Rotation of a Constraint ............................. 110
6.2.1 The Rotation Procedure ............................. 1ll
6.3 Constraint Generation .................................... 112
6.3.1. The Modified Lifting Procedure .................... 114
6.4 Benders' Decomposition ................................... 115
6.5 The Primal-Dual Decomposition ............................ 117
6.6 The Knapsack Problem and the Shortest Path Problem ....... 119
6.7 Bibliographic Notes ...................................... 119
6.8 Exercises ................................................ 120
CHAPTER 7. Relaxations of Integer Problems. Duality ........... 122
7.1 Lagrangean Relaxations ................................... 122
7.1.1 Properties of a Lagrangean Relaxation ............. 123
7.1.2 Calculating Lagrangean Multipliers ................ 125
7.1.3 Using Lagrangean Relaxation in Branch-and-Bound
Methods ........................................... 127
7.2 Surrogate Problems ....................................... 127
7.3 The Generalized Assignment Problem ....................... 129
7.4 Price Functions .......................................... 131
7.4.1 Perturbation Functions ............................ 132
7.4.2 Optimality Conditions and Economic
Interpretations ................................... 133
7.5 Duality in Integer Programming ........................... 134
7.6 Remarks about Sensitivity Analysis ....................... 135
7.7 Duality and Constraint Aggregation ....................... 136
7.8 Bibliographic Notes ...................................... 137
7.9 Exercises ................................................ 138
CHAPTER 8. Some Particular Integer Programming Problems ....... 140
8.1 Packing, Partitioning and Covering Problems .............. 140
8.1.1 Basic Properties .................................. 141
8.1.2 A Transformation of the Knapsack Problem into
the Set Packing Problem ........................... 142
8.1.3 Reductions ........................................ 143
8.2 Optimization Problems over Graphs ........................ 144
8.3 Packing and Covering Polytopes ........................... 145
8.4 The Travelling Salesman Problem .......................... 147
8.5 Methods for TSP .......................................... 149
8.6 Bibliographic Notes ...................................... 151
8.7 Exercises ................................................ 151
CHAPTER 9. Near-Optimal Methods ............................... 153
9.1 Classification and Evaluation of Near-Optimal Methods .... 153
9.2 An Analysis of the Greedy Algorithm ...................... 155
9.3 Approximation Methods .................................... 157
9.3.1 A Polynomial Approximation Scheme ................. 157
9.3.2 Fully Polynomial Approximation Schemes ............ 158
9.4 Near-Optimal Methods for TSP ............................. 160
9.5 Independence Systems and Matroids ........................ 161
9.6 Bibliographic Notes ...................................... 165
9.7 Exercises ................................................ 166
CHAPTER 10. Conclusions ....................................... 167
10.1 Computer Codes .......................................... 167
10.2 Future Trends ........................................... 169
Bibliography .................................................. 170
Index ......................................................... 179
|
