Introduction ................................................... ix
Acknowledgments .............................................. xiii
1. Definitions .................................................. 1
1.1. Holomorphic functions and tangent spaces ............... 1
1.2. Analytic subsets ....................................... 2
1.3. Hulls of compact sets .................................. 2
1.4. Harmonic, pluriharmonic and plurisubharmonic
functions .............................................. 2
1.5. CR-geometry ............................................ 3
1.6. The Levi-form and Levi-convexity ....................... 4
1.7. Representation formulas ................................ 9
1.7.1. The Cauchy kernel .............................. 9
1.7.2. The Bergman kernel ............................. 9
1.7.3. The Bochner-Martinelli kernel ................. 11
1.7.4. The Henkin kernel ............................. 11
2. Classical extension theorems in one and several complex
variables ................................................... 13
2.1. Basic theorems ........................................ 13
2.2. Extension theorems in one complex variable ............ 14
2.2.1. Removable singularities for bounded
holomorphic functions ......................... 14
2.2.2. Reflection principle .......................... 15
2.3. Extension theorems in several complex variable ........ 15
2.3.1. Extension near small-dimensional sets ......... 15
2.3.2. Edge of the wedge theorem ..................... 17
3. Extension of CR-functions up to a Levi-flat boundary
and of holomorphic maps ..................................... 21
3.1. Global extension for CR-functions ..................... 21
3.2. Local extension for СR-functions ...................... 22
3.3. Extension up to a Levi-flat boundary .................. 22
3.4. Extension out of holomorphic hulls .................... 26
3.5. Extension in Stein manifolds .......................... 33
3.6. Extension on unbounded domains ........................ 33
3.7. Extension of holomorphic maps: the reflection
principle in higher dimension ......................... 34
3.7.1. Reflection principle in 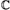 ..................... 35
3.7.2. Reflection principle and extension theorems
in ..................... 35
3.7.2. Reflection principle and extension theorems
in 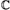 n, n > 1 .................................. 37
3.7.3. Extension in the strictly pseudoconvex
case .......................................... 38
3.7.4. Holomorphic extension in dimension n = 2 ...... 39
3.7.5. Extension of proper holomorphic maps between
strictly pseudoconvex Сω-domains .............. 40
3.7.6. Algebroid functions ........................... 42
3.7.7. Edge of the wedge theorem for the cotangent
bundle ........................................ 43
3.7.8. Scaling method ................................ 44
3.7.9. Non-pseudoconvex case ......................... 46
3.7.10. Main Theorems ................................. 46
3.7.11. Properties of Segre varieties ................. 49
3.7.12. Complex structure of the set of Segre
varieties ..................................... 50
3.7.13. Extending the graph of ƒ ...................... 51
3.7.14. Conclusion of proof ........................... 52
3.7.15. Final considerations .......................... 53
4. Cohomology vanishing and extension problems for semi
q-coronae ................................................... 57
4.1. Introduction .......................................... 57
4.2. Cohomology and extension of sections .................. 59
4.2.1. Closed q-coronae .............................. 59
4.2.2. Open q-coronae ................................ 61
4.2.3. Corollaries of the extension theorems ......... 64
4.3. Extension of divisors and analytic sets of
codimension one ....................................... 67
5. Cohomology of semi 1-coronae and extension of analytic
subsets ..................................................... 73
5.1. Introduction .......................................... 73
5.2. Remarks on the proofs of theorems in Chapter 4 ........ 74
5.3. An isomorphism theorem for complete semi 1-coronae .... 76
5.3.1. Bump lemma: surjectivity of cohomology ........ 77
5.3.2. Approximation ................................. 80
5.4. Extension of coherent sheaves and analytic subsets .... 85
5.5. Some generalizations .................................. 88
5.5.1. Bump lemma for semi q-coronae ................. 88
5.5.2. Semi q-coronae in Stein spaces ................ 89
6. The boundary problem ........................................ 91
6.1. The boundary problem .................................. 91
6.2. The boundary problem for compact curves ............... 92
6.2.1. Sketches of the proofs ........................ 92
6.2.2. Generalization to several curves .............. 97
6.3. The boundary problem for compact manifolds ............ 97
6.3.1. The boundary problem in terms of holomorphic
chains ........................................ 97
6.3.2. The boundary problem in strictly
pseudoconvex domains ......................... 100
6.3.3. The boundary problem and the linking
number ....................................... 100
6.4. The boundary problem in q-concave domains ............ 101
6.5. The boundary problem in n, n > 1 .................................. 37
3.7.3. Extension in the strictly pseudoconvex
case .......................................... 38
3.7.4. Holomorphic extension in dimension n = 2 ...... 39
3.7.5. Extension of proper holomorphic maps between
strictly pseudoconvex Сω-domains .............. 40
3.7.6. Algebroid functions ........................... 42
3.7.7. Edge of the wedge theorem for the cotangent
bundle ........................................ 43
3.7.8. Scaling method ................................ 44
3.7.9. Non-pseudoconvex case ......................... 46
3.7.10. Main Theorems ................................. 46
3.7.11. Properties of Segre varieties ................. 49
3.7.12. Complex structure of the set of Segre
varieties ..................................... 50
3.7.13. Extending the graph of ƒ ...................... 51
3.7.14. Conclusion of proof ........................... 52
3.7.15. Final considerations .......................... 53
4. Cohomology vanishing and extension problems for semi
q-coronae ................................................... 57
4.1. Introduction .......................................... 57
4.2. Cohomology and extension of sections .................. 59
4.2.1. Closed q-coronae .............................. 59
4.2.2. Open q-coronae ................................ 61
4.2.3. Corollaries of the extension theorems ......... 64
4.3. Extension of divisors and analytic sets of
codimension one ....................................... 67
5. Cohomology of semi 1-coronae and extension of analytic
subsets ..................................................... 73
5.1. Introduction .......................................... 73
5.2. Remarks on the proofs of theorems in Chapter 4 ........ 74
5.3. An isomorphism theorem for complete semi 1-coronae .... 76
5.3.1. Bump lemma: surjectivity of cohomology ........ 77
5.3.2. Approximation ................................. 80
5.4. Extension of coherent sheaves and analytic subsets .... 85
5.5. Some generalizations .................................. 88
5.5.1. Bump lemma for semi q-coronae ................. 88
5.5.2. Semi q-coronae in Stein spaces ................ 89
6. The boundary problem ........................................ 91
6.1. The boundary problem .................................. 91
6.2. The boundary problem for compact curves ............... 92
6.2.1. Sketches of the proofs ........................ 92
6.2.2. Generalization to several curves .............. 97
6.3. The boundary problem for compact manifolds ............ 97
6.3.1. The boundary problem in terms of holomorphic
chains ........................................ 97
6.3.2. The boundary problem in strictly
pseudoconvex domains ......................... 100
6.3.3. The boundary problem and the linking
number ....................................... 100
6.4. The boundary problem in q-concave domains ............ 101
6.5. The boundary problem in 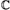  n .......................... 102
6.5.1. The projective hull .......................... 103
6.5.2. The projective linking number ................ 104
6.5.3. l-sheeted solutions .......................... 106
6.6. The boundary problem for non-compact cycles .......... 106
6.7. The boundary problem in an arbitrary complex
manifold X ........................................... 107
7. Non-compact boundaries of complex analytic varieties ....... 109
7.1. Introduction ......................................... 109
7.2. The local result ..................................... 111
7.3. The global result .................................... 115
7.3.1. M is of dimension at least 5 (m ≥ 2) ......... 116
7.3.2. M is of dimension 3 (m = 1) .................. 120
7.3.3. M is of dimension 1 (m = 0) .................. 122
7.4. Extension to pseudoconvex domains .................... 122
7.5. On the Lupacciolu's (*) condition .................... 124
8. Semi-local extension of maximally complex submanifolds ..... 125
8.1. Introduction ......................................... 125
8.2. Main result .......................................... 126
8.2.1. M is of dimension at least 5 (m ≥ 2) ......... 127
8.2.2. M is of dimension 3 (m = 1) .................. 131
8.3. Some remarks ......................................... 134
8.3.1. Maximality of the solution ................... 134
8.3.2. The unbounded case ........................... 135
8.4. Generalization to analytic sets ...................... 136
References .................................................... 141 n .......................... 102
6.5.1. The projective hull .......................... 103
6.5.2. The projective linking number ................ 104
6.5.3. l-sheeted solutions .......................... 106
6.6. The boundary problem for non-compact cycles .......... 106
6.7. The boundary problem in an arbitrary complex
manifold X ........................................... 107
7. Non-compact boundaries of complex analytic varieties ....... 109
7.1. Introduction ......................................... 109
7.2. The local result ..................................... 111
7.3. The global result .................................... 115
7.3.1. M is of dimension at least 5 (m ≥ 2) ......... 116
7.3.2. M is of dimension 3 (m = 1) .................. 120
7.3.3. M is of dimension 1 (m = 0) .................. 122
7.4. Extension to pseudoconvex domains .................... 122
7.5. On the Lupacciolu's (*) condition .................... 124
8. Semi-local extension of maximally complex submanifolds ..... 125
8.1. Introduction ......................................... 125
8.2. Main result .......................................... 126
8.2.1. M is of dimension at least 5 (m ≥ 2) ......... 127
8.2.2. M is of dimension 3 (m = 1) .................. 131
8.3. Some remarks ......................................... 134
8.3.1. Maximality of the solution ................... 134
8.3.2. The unbounded case ........................... 135
8.4. Generalization to analytic sets ...................... 136
References .................................................... 141
|