Preface to the second edition ................................. vii
Preface to the first edition ................................... ix
1 Hyperbolic geometry of the unit disc ......................... 1
1.1 Hyperbolic geometry of the unit disc .................... 1
1.2 Some applications ...................................... 12
1.3 Exercises .............................................. 18
1.4 List of problems ....................................... 19
2 The Caratheodory pseudodistance and the Caratheodory-
Reiffen pseudometric ........................................ 20
2.1 Definitions. General Schwarz-Pick lemma ................ 21
2.2 Balanced domains ....................................... 24
2.2.1 Operator ɧ → 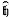 .................................. 26
2.2.2 Operator ɧ → .................................. 26
2.2.2 Operator ɧ → 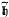 .................................. 30
2.2.3 Operator ɧ → .................................. 30
2.2.3 Operator ɧ → 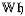 ................................ 31
2.2.4 d -balanced domains ............................. 38
2.3 Caratheodory pseudodistance and pseudometric in
balanced domains ....................................... 39
2.4 Caratheodory isometries ................................ 46
2.5 Caratheodory hyperbolicity ............................. 53
2.6 The Caratheodory topology .............................. 54
2.7 Properties of c(*) and γ. Length of curve. Inner
Carathéodory pseudodistance ............................ 58
2.8 ci-hyperbolicity versus с-hyperbolicity ................ 73
2.9 Two applications ....................................... 75
2.10 A class of n-circled domains ........................... 79
2.11 Neile parabola ......................................... 92
2.12 Exercises ............................................. 100
2.13 List of problems ...................................... 105
3 Kobayashi pseudodistance and the Kobayashi-Royden
peeodometric ............................................... 106
3.1 The Lempert function and the Kobayashi
pseudodistance ........................................ 106
3.2 Tautness .............................................. 112
3.3 General properties of k ............................... 119
3.4 An extension theorem .................................. 124
3.5 The Kobayashi-Royden pseudometric ..................... 126
3.6 The Kobayashi-Buseman pseudometric ................... 135
3.7 Product formula ....................................... 141
3.8 Higher-order Lempert functions and Kobayashi-Royden
pseudometrics ......................................... 143
3.9 Exercises ............................................. 147
3.10 List of problems ...................................... 149
4 Contractible systems ....................................... 150
4.1 Abstract point of view ................................ 150
4.2 Extremal problems for plurisubharmonic functions ...... 154
4.2.1 Properties of gG and AG ........................ 159
4.2.2 Examples ....................................... 169
4.2.3 Properties of SG ............................... 173
4.2.4 Properties of mG(k) and γG(k) .................... 175
4.3 Inner pseudodistances. Integrated forms.
Derivatives. Buseman pseudometrics. ................................ 31
2.2.4 d -balanced domains ............................. 38
2.3 Caratheodory pseudodistance and pseudometric in
balanced domains ....................................... 39
2.4 Caratheodory isometries ................................ 46
2.5 Caratheodory hyperbolicity ............................. 53
2.6 The Caratheodory topology .............................. 54
2.7 Properties of c(*) and γ. Length of curve. Inner
Carathéodory pseudodistance ............................ 58
2.8 ci-hyperbolicity versus с-hyperbolicity ................ 73
2.9 Two applications ....................................... 75
2.10 A class of n-circled domains ........................... 79
2.11 Neile parabola ......................................... 92
2.12 Exercises ............................................. 100
2.13 List of problems ...................................... 105
3 Kobayashi pseudodistance and the Kobayashi-Royden
peeodometric ............................................... 106
3.1 The Lempert function and the Kobayashi
pseudodistance ........................................ 106
3.2 Tautness .............................................. 112
3.3 General properties of k ............................... 119
3.4 An extension theorem .................................. 124
3.5 The Kobayashi-Royden pseudometric ..................... 126
3.6 The Kobayashi-Buseman pseudometric ................... 135
3.7 Product formula ....................................... 141
3.8 Higher-order Lempert functions and Kobayashi-Royden
pseudometrics ......................................... 143
3.9 Exercises ............................................. 147
3.10 List of problems ...................................... 149
4 Contractible systems ....................................... 150
4.1 Abstract point of view ................................ 150
4.2 Extremal problems for plurisubharmonic functions ...... 154
4.2.1 Properties of gG and AG ........................ 159
4.2.2 Examples ....................................... 169
4.2.3 Properties of SG ............................... 173
4.2.4 Properties of mG(k) and γG(k) .................... 175
4.3 Inner pseudodistances. Integrated forms.
Derivatives. Buseman pseudometrics.
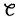 1-pseudodistances ................................... 180
4.3.1 Operator d → d1 ................................ 181
4.3.2 Operator δ → ∫δ ................................ 183
4.3.3 Operator d → 1-pseudodistances ................................... 180
4.3.1 Operator d → d1 ................................ 181
4.3.2 Operator δ → ∫δ ................................ 183
4.3.3 Operator d → 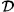 d ............................... 184
4.3.4 Operator δ → d ............................... 184
4.3.4 Operator δ → 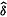 ................................. 186
4.3.5 Operator δ → ................................. 186
4.3.5 Operator δ → 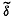 ................................ 188
4.3.6 ................................ 188
4.3.6 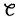 1-pseudodistances ............................ 190
4.4 Exercises ............................................. 192
4.5 List of problems ...................................... 193
5 Properties of standard contractible systems ................ 194
5.1 Regularity properties of gG and AG .................... 194
5.2 Lipschitz continuity of ℓ*, x, g, and A ............... 199
5.3 Derivatives ........................................... 210
5.4 List of problems ...................................... 221
6 Elementary Reinhardt domains ............................... 222
6.1 Elementary n-circled domains .......................... 222
6.2 General point of view ................................. 225
6.3 Elementary n-circled domains II ....................... 237
6.4 Exercises ............................................. 244
6.5 List of problems ...................................... 245
7 Symmetrized polydisc ....................................... 246
7.1 Symmetrized bidisc .................................... 246
7.2 Symmetrized polydisc .................................. 263
7.3 List of problems ...................................... 275
8 Non-standard contractible systems .......................... 276
8.1 Hahn function and pseudometric ........................ 276
8.2 Generalized Green, Mцbius, and Lempert functions ...... 291
8.3 Wu pseudometric ....................................... 321
8.4 Exercises ............................................. 327
8.5 List of problems ...................................... 328
9 Contractible functions and metrics for the annulus ......... 329
9.1 Contractible functions and metrics for the annulus .... 329
9.2 Exercises ............................................. 340
9.3 List of problems ...................................... 343
10 Elementary it-circled domains III .......................... 344
10.1 Elementary n-circled domains III ...................... 344
10.2 List of problems ...................................... 357
11 Complex geodesies. Lempert's theorem ....................... 358
11.1 Complex geodesies ..................................... 359
11.2 Lempert's theorem ..................................... 365
11.3 Uniqueness of complex geodesies ....................... 379
11.4 Poletsky-Edigarian theorem ............................ 385
11.4.1 Proof of Theorem 11.4.5 ........................ 389
11.5 Schwarz lemma - the case of equality .................. 398
11.6 Criteria for biholomorphicity ......................... 401
11.7 Exercises ............................................. 404
11.8 List of problems ...................................... 409
12 The Bergman metric ......................................... 410
12.1 The Bergman kernel .................................... 410
12.2 Minimal ball .......................................... 434
12.3 The Lu Qi-Keng problem ................................ 446
12.4 Bergman exhaustiveness ................................ 454
12.5 Bergman exhaustiveness II - plane domains ............. 461
12.6 Lh2-domains of holomorphy .............................. 478
12.7 The Bergman pseudometric .............................. 482
12.8 Comparison and localization ........................... 490
12.9 The Skwarczyński pseudometric ......................... 494
12.10 Exercises ............................................ 497
12.11 List of problems ..................................... 499
13 Hyperbolicity .............................................. 500
13.1 Global hyperbolicity .................................. 500
13.2 Local hyperbolicity ................................... 506
13.3 Hyperbolicity for Reinhardt domains ................... 511
13.4 Hyperbolicities for balanced domains .................. 518
13.5 Hyperbolicities for Hartogs type domains .............. 521
13.6 Hyperbolicities for tube domains ...................... 523
13.7 Exercises ............................................. 532
13.8 List of problems ...................................... 533
14 Completeness ............................................... 534
14.1 Completeness - general discussion ..................... 534
14.2 Caratheodory completeness ............................. 538
14.3 с-completeness for Reinhardt domains .................. 544
14.4 ∫γ(k)-completeness for Zalcman domains ................ 554
14.5 Kobayashi completeness ................................ 563
14.6 Exercises ............................................. 570
14.7 List of problems ...................................... 571
15 Bergman completeness ....................................... 573
15.1 Bergman completeness .................................. 573
15.2 Reinhardt domains and й-completeness .................. 585
15.3 List of problems ...................................... 591
16 Complex geodesies - effective examples ..................... 592
16.1 Complex geodesies in the classical unit balls ......... 592
16.2 Geodesies in convex complex ellipsoids ................ 594
16.3 Extremal discs in arbitrary complex ellipsoids ........ 604
16.4 Biholomorphisms of complex ellipsoids ................. 608
16.5 Complex geodesies in the minimal ball ................. 611
16.6 Effective formula for the Kobayashi-Royden metric
in certain complex ellipsoids ......................... 624
16.6.1 Formula for xε((1)m)) ............................ 624
16.6.2 Formula for xε((1/2,1/2)) ......................... 631
16.7 Complex geodesies in the symmetrized bidisc ........... 633
16.8 Complex geodesies in the tetrablock ................... 640
16.9 Exercises ............................................. 642
16.10 List of problems ..................................... 643
17 Analytic discs method ...................................... 644
17.1 Relative extremal function ............................ 644
17.2 Disc functionals ...................................... 647
17.3 Poisson functional .................................... 649
17.4 Green, Lelong, and Lempert functionals ................ 654
17.5 Exercises ............................................. 666
18 Product property ........................................... 667
18.1 Product property - general theory ..................... 667
18.2 Product property for the Möbius functions ............. 672
18.3 Product property for the generalized Mцbius function .. 676
18.4 Product property for the Green function ............... 679
18.5 Product property for the relative extremal function ... 680
18.6 Product property for the generalized Green function ... 686
18.7 Product property for the generalized Lempert
function .............................................. 688
18.8 Exercises ............................................. 689
18.9 List of problems ...................................... 690
19 Comparison on pseudoconvex domains ......................... 691
19.1 Strongly pseudoconvex domains ......................... 692
19.2 The boundary behavior of the Caratheodory and the
Kobayashi distances ................................... 697
19.3 Localization .......................................... 705
19.4 Boundary behavior of the Carathéodory-Reiffen and
the Kobayashi-Royden metrics .......................... 710
19.5 A comparison of distances ............................. 720
19.6 Characterization of the unit ball by its
automorphism group .................................... 722
19.7 Exercises ............................................. 729
19.8 List of problems ...................................... 730
20 Boundary behavior of invariant functions and metrics on
general domains ............................................ 731
20.1 Boundary behavior of pseudometrics for non
pseudoconvex domains .................................. 731
20.2 Boundary behavior of x on pseudoconvex domains in
normal direction ...................................... 741
20.3 An upper boundary estimate for the Lempert function ... 751
20.4 Exercises ............................................. 764
20.5 List of problems ...................................... 764
A Miscellanea ................................................ 765
A.l Caratheodory balls ..................................... 765
A.2 The automorphism group of bounded domains .............. 766
A.3 Symmetrized ellipsoids ................................. 767
A.4 Holomorphic curvature .................................. 769
A.5 Complex geodesies ...................................... 772
A.6 Criteria for biholomorphicity .......................... 775
A.7 Isometries ............................................. 777
A.8 Boundary behavior of contractible metrics on weakly
pseudoconvex domains ................................... 778
A.9 Spectral ball .......................................... 783
A.10 List of problems ...................................... 784
В Addendum ................................................... 785
B.l Holomorphic functions ................................. 785
В.1.1 Analytic sets .................................. 788
B.2 Proper holomorphic mappings ........................... 789
B.3 Automorphisms ......................................... 789
B.3.1 Automorphisms of the unit disc ................. 789
B.3.2 Automorphisms of the unit polydisc ............. 790
B.3.3 Automorphisms of the unit Euclidean ball ....... 790
B.4 Subharmonic and plurisubharmonic functions ............ 791
B.5 Green function and Dirichlet problem .................. 795
B.6 Monge-Ampere operator ................................. 798
B.7 Domains of holomorphy and pseudoconvex domains ........ 799
B.7.1 Stein manifolds ................................ 803
B.8 L2-holomorphic functions .............................. 804
B.9 Hardy spaces .......................................... 805
B.10 Kronecker theorem ..................................... 808
B.ll List of problems ...................................... 808
С List of problems ........................................... 809
Bibliography .................................................. 814
List of symbols ............................................... 843
Index ......................................................... 854 1-pseudodistances ............................ 190
4.4 Exercises ............................................. 192
4.5 List of problems ...................................... 193
5 Properties of standard contractible systems ................ 194
5.1 Regularity properties of gG and AG .................... 194
5.2 Lipschitz continuity of ℓ*, x, g, and A ............... 199
5.3 Derivatives ........................................... 210
5.4 List of problems ...................................... 221
6 Elementary Reinhardt domains ............................... 222
6.1 Elementary n-circled domains .......................... 222
6.2 General point of view ................................. 225
6.3 Elementary n-circled domains II ....................... 237
6.4 Exercises ............................................. 244
6.5 List of problems ...................................... 245
7 Symmetrized polydisc ....................................... 246
7.1 Symmetrized bidisc .................................... 246
7.2 Symmetrized polydisc .................................. 263
7.3 List of problems ...................................... 275
8 Non-standard contractible systems .......................... 276
8.1 Hahn function and pseudometric ........................ 276
8.2 Generalized Green, Mцbius, and Lempert functions ...... 291
8.3 Wu pseudometric ....................................... 321
8.4 Exercises ............................................. 327
8.5 List of problems ...................................... 328
9 Contractible functions and metrics for the annulus ......... 329
9.1 Contractible functions and metrics for the annulus .... 329
9.2 Exercises ............................................. 340
9.3 List of problems ...................................... 343
10 Elementary it-circled domains III .......................... 344
10.1 Elementary n-circled domains III ...................... 344
10.2 List of problems ...................................... 357
11 Complex geodesies. Lempert's theorem ....................... 358
11.1 Complex geodesies ..................................... 359
11.2 Lempert's theorem ..................................... 365
11.3 Uniqueness of complex geodesies ....................... 379
11.4 Poletsky-Edigarian theorem ............................ 385
11.4.1 Proof of Theorem 11.4.5 ........................ 389
11.5 Schwarz lemma - the case of equality .................. 398
11.6 Criteria for biholomorphicity ......................... 401
11.7 Exercises ............................................. 404
11.8 List of problems ...................................... 409
12 The Bergman metric ......................................... 410
12.1 The Bergman kernel .................................... 410
12.2 Minimal ball .......................................... 434
12.3 The Lu Qi-Keng problem ................................ 446
12.4 Bergman exhaustiveness ................................ 454
12.5 Bergman exhaustiveness II - plane domains ............. 461
12.6 Lh2-domains of holomorphy .............................. 478
12.7 The Bergman pseudometric .............................. 482
12.8 Comparison and localization ........................... 490
12.9 The Skwarczyński pseudometric ......................... 494
12.10 Exercises ............................................ 497
12.11 List of problems ..................................... 499
13 Hyperbolicity .............................................. 500
13.1 Global hyperbolicity .................................. 500
13.2 Local hyperbolicity ................................... 506
13.3 Hyperbolicity for Reinhardt domains ................... 511
13.4 Hyperbolicities for balanced domains .................. 518
13.5 Hyperbolicities for Hartogs type domains .............. 521
13.6 Hyperbolicities for tube domains ...................... 523
13.7 Exercises ............................................. 532
13.8 List of problems ...................................... 533
14 Completeness ............................................... 534
14.1 Completeness - general discussion ..................... 534
14.2 Caratheodory completeness ............................. 538
14.3 с-completeness for Reinhardt domains .................. 544
14.4 ∫γ(k)-completeness for Zalcman domains ................ 554
14.5 Kobayashi completeness ................................ 563
14.6 Exercises ............................................. 570
14.7 List of problems ...................................... 571
15 Bergman completeness ....................................... 573
15.1 Bergman completeness .................................. 573
15.2 Reinhardt domains and й-completeness .................. 585
15.3 List of problems ...................................... 591
16 Complex geodesies - effective examples ..................... 592
16.1 Complex geodesies in the classical unit balls ......... 592
16.2 Geodesies in convex complex ellipsoids ................ 594
16.3 Extremal discs in arbitrary complex ellipsoids ........ 604
16.4 Biholomorphisms of complex ellipsoids ................. 608
16.5 Complex geodesies in the minimal ball ................. 611
16.6 Effective formula for the Kobayashi-Royden metric
in certain complex ellipsoids ......................... 624
16.6.1 Formula for xε((1)m)) ............................ 624
16.6.2 Formula for xε((1/2,1/2)) ......................... 631
16.7 Complex geodesies in the symmetrized bidisc ........... 633
16.8 Complex geodesies in the tetrablock ................... 640
16.9 Exercises ............................................. 642
16.10 List of problems ..................................... 643
17 Analytic discs method ...................................... 644
17.1 Relative extremal function ............................ 644
17.2 Disc functionals ...................................... 647
17.3 Poisson functional .................................... 649
17.4 Green, Lelong, and Lempert functionals ................ 654
17.5 Exercises ............................................. 666
18 Product property ........................................... 667
18.1 Product property - general theory ..................... 667
18.2 Product property for the Möbius functions ............. 672
18.3 Product property for the generalized Mцbius function .. 676
18.4 Product property for the Green function ............... 679
18.5 Product property for the relative extremal function ... 680
18.6 Product property for the generalized Green function ... 686
18.7 Product property for the generalized Lempert
function .............................................. 688
18.8 Exercises ............................................. 689
18.9 List of problems ...................................... 690
19 Comparison on pseudoconvex domains ......................... 691
19.1 Strongly pseudoconvex domains ......................... 692
19.2 The boundary behavior of the Caratheodory and the
Kobayashi distances ................................... 697
19.3 Localization .......................................... 705
19.4 Boundary behavior of the Carathéodory-Reiffen and
the Kobayashi-Royden metrics .......................... 710
19.5 A comparison of distances ............................. 720
19.6 Characterization of the unit ball by its
automorphism group .................................... 722
19.7 Exercises ............................................. 729
19.8 List of problems ...................................... 730
20 Boundary behavior of invariant functions and metrics on
general domains ............................................ 731
20.1 Boundary behavior of pseudometrics for non
pseudoconvex domains .................................. 731
20.2 Boundary behavior of x on pseudoconvex domains in
normal direction ...................................... 741
20.3 An upper boundary estimate for the Lempert function ... 751
20.4 Exercises ............................................. 764
20.5 List of problems ...................................... 764
A Miscellanea ................................................ 765
A.l Caratheodory balls ..................................... 765
A.2 The automorphism group of bounded domains .............. 766
A.3 Symmetrized ellipsoids ................................. 767
A.4 Holomorphic curvature .................................. 769
A.5 Complex geodesies ...................................... 772
A.6 Criteria for biholomorphicity .......................... 775
A.7 Isometries ............................................. 777
A.8 Boundary behavior of contractible metrics on weakly
pseudoconvex domains ................................... 778
A.9 Spectral ball .......................................... 783
A.10 List of problems ...................................... 784
В Addendum ................................................... 785
B.l Holomorphic functions ................................. 785
В.1.1 Analytic sets .................................. 788
B.2 Proper holomorphic mappings ........................... 789
B.3 Automorphisms ......................................... 789
B.3.1 Automorphisms of the unit disc ................. 789
B.3.2 Automorphisms of the unit polydisc ............. 790
B.3.3 Automorphisms of the unit Euclidean ball ....... 790
B.4 Subharmonic and plurisubharmonic functions ............ 791
B.5 Green function and Dirichlet problem .................. 795
B.6 Monge-Ampere operator ................................. 798
B.7 Domains of holomorphy and pseudoconvex domains ........ 799
B.7.1 Stein manifolds ................................ 803
B.8 L2-holomorphic functions .............................. 804
B.9 Hardy spaces .......................................... 805
B.10 Kronecker theorem ..................................... 808
B.ll List of problems ...................................... 808
С List of problems ........................................... 809
Bibliography .................................................. 814
List of symbols ............................................... 843
Index ......................................................... 854
|