Preliminaries: before we begin ............................... 1
Sets and set notation ........................................ 1
Numbers ...................................................... 2
Mathematical terminology ..................................... 3
Basic algebra ................................................ 4
Trigonometry ................................................. 7
A little bit of logic ........................................ 8
1 Matrices and vectors ........................................ 10
1.1 What is a matrix? ...................................... 10
1.2 Matrix addition and scalar multiplication .............. 11
1.3 Matrix multiplication .................................. 12
1.4 Matrix algebra ......................................... 14
1.5 Matrix inverses ........................................ 16
1.6 Powers of a matrix ..................................... 20
1.7 The transpose and symmetric matrices ................... 20
1.8 Vectors in 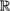 n .......................................... 23
1.9 Developing geometric insight ........................... 27
1.10 Lines .................................................. 33
1.11 Planes in n .......................................... 23
1.9 Developing geometric insight ........................... 27
1.10 Lines .................................................. 33
1.11 Planes in 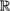 n ........................................... 39
1.12 Lines and hyperplanes in n ........................................... 39
1.12 Lines and hyperplanes in 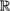 n ............................ 46
1.13 Learning outcomes ...................................... 47
1.14 Comments on activities ................................. 48
1.15 Exercises .............................................. 53
1.16 Problems ............................................... 55
2 Systems of linear equations ................................. 59
2.1 Systems of linear equations ............................ 59
2.2 Row operations ......................................... 62
2.3 Gaussian elimination ................................... 64
2.4 Homogeneous systems and null space ..................... 75
2.5 Learning outcomes ...................................... 81
2.6 Comments on activities ................................. 82
2.7 Exercises .............................................. 84
2.8 Problems ............................................... 86
3 Matrix inversion and determinants ........................... 90
3.1 Matrix inverse using row operations .................... 90
3.2 Determinants ........................................... 98
3.3 Results on determinants ............................... 104
3.4 Matrix inverse using cofactors ........................ 113
3.5 Leontief input-output analysis ........................ 119
3.6 Learning outcomes ..................................... 121
3.7 Comments on activities ................................ 122
3.8 Exercises ............................................. 125
3.9 Problems .............................................. 128
4 Rank, range and linear equations ........................... 131
4.1 The rank of a matrix .................................. 131
4.2 Rank and systems of linear equations .................. 133
4.3 Range ................................................. 139
4.4 Learning outcomes ..................................... 142
4.5 Comments on activities ................................ 142
4.6 Exercises ............................................. 144
4.7 Problems .............................................. 146
5 Vector spaces .............................................. 149
5.1 Vector spaces ......................................... 149
5.2 Subspaces ............................................. 154
5.3 Linear span ........................................... 160
5.4 Learning outcomes ..................................... 164
5.5 Comments on activities ................................ 164
5.6 Exercises ............................................. 168
5.7 Problems .............................................. 170
6 Linear independence, bases and dimension ................... 172
6.1 Linear independence ................................... 172
6.2 Bases ................................................. 181
6.3 Coordinates ........................................... 185
6.4 Dimension ............................................. 186
6.5 Basis and dimension in n ............................ 46
1.13 Learning outcomes ...................................... 47
1.14 Comments on activities ................................. 48
1.15 Exercises .............................................. 53
1.16 Problems ............................................... 55
2 Systems of linear equations ................................. 59
2.1 Systems of linear equations ............................ 59
2.2 Row operations ......................................... 62
2.3 Gaussian elimination ................................... 64
2.4 Homogeneous systems and null space ..................... 75
2.5 Learning outcomes ...................................... 81
2.6 Comments on activities ................................. 82
2.7 Exercises .............................................. 84
2.8 Problems ............................................... 86
3 Matrix inversion and determinants ........................... 90
3.1 Matrix inverse using row operations .................... 90
3.2 Determinants ........................................... 98
3.3 Results on determinants ............................... 104
3.4 Matrix inverse using cofactors ........................ 113
3.5 Leontief input-output analysis ........................ 119
3.6 Learning outcomes ..................................... 121
3.7 Comments on activities ................................ 122
3.8 Exercises ............................................. 125
3.9 Problems .............................................. 128
4 Rank, range and linear equations ........................... 131
4.1 The rank of a matrix .................................. 131
4.2 Rank and systems of linear equations .................. 133
4.3 Range ................................................. 139
4.4 Learning outcomes ..................................... 142
4.5 Comments on activities ................................ 142
4.6 Exercises ............................................. 144
4.7 Problems .............................................. 146
5 Vector spaces .............................................. 149
5.1 Vector spaces ......................................... 149
5.2 Subspaces ............................................. 154
5.3 Linear span ........................................... 160
5.4 Learning outcomes ..................................... 164
5.5 Comments on activities ................................ 164
5.6 Exercises ............................................. 168
5.7 Problems .............................................. 170
6 Linear independence, bases and dimension ................... 172
6.1 Linear independence ................................... 172
6.2 Bases ................................................. 181
6.3 Coordinates ........................................... 185
6.4 Dimension ............................................. 186
6.5 Basis and dimension in 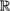 n ............................. 191
6.6 Learning outcomes ..................................... 199
6.7 Comments on activities ................................ 199
6.8 Exercises ............................................. 202
6.9 Problems .............................................. 205
7 Linear transformations and change of basis ................. 210
7.1 Linear transformations ................................ 210
7.2 Range and null space .................................. 220
7.3 Coordinate change ..................................... 223
7.4 Change of basis and similarity ........................ 229
7.5 Learning outcomes ..................................... 235
7.6 Comments on activities ................................ 235
7.7 Exercises ............................................. 239
7.8 Problems .............................................. 242
8 Diagonalisation ............................................ 247
8.1 Eigenvalues and eigenvectors .......................... 247
8.2 Diagonalisation of a square matrix .................... 256
8.3 When is diagonalisation possible? ..................... 263
8.4 Learning outcomes ..................................... 272
8.5 Comments on activities ................................ 273
8.6 Exercises ............................................. 274
8.7 Problems .............................................. 276
9 Applications of diagonalisation ............................ 279
9.1 Powers of matrices .................................... 279
9.2 Systems of difference equations ....................... 282
9.3 Linear systems of differential equations .............. 296
9.4 Learning outcomes ..................................... 303
9.5 Comments on activities ................................ 303
9.6 Exercises ............................................. 305
9.7 Problems .............................................. 308
10 Inner products and orthogonality ........................... 312
10.1 Inner products ........................................ 312
10.2 Orthogonality ......................................... 316
10.3 Orthogonal matrices ................................... 319
10.4 Gram-Schmidt orthonormalisation process ............... 321
10.5 Learning outcomes ..................................... 323
10.6 Comments on activities ................................ 324
10.7 Exercises ............................................. 325
10.8 Problems .............................................. 326
11 Orthogonal diagonalisation and its applications ............ 329
11.1 Orthogonal diagonalisation of symmetric matrices ...... 329
11.2 Quadratic forms ....................................... 339
11.3 Learning outcomes ..................................... 355
11.4 Comments on activities ................................ 356
11.5 Exercises ............................................. 358
11.6 Problems .............................................. 360
12 Direct sums and projections ................................ 364
12.1 The direct sum of two subspaces ....................... 364
12.2 Orthogonal complements ................................ 367
12.3 Projections ........................................... 372
12.4 Characterising projections and orthogonal
projections ........................................... 374
12.5 Orthogonal projection onto the range of a matrix ...... 376
12.6 Minimising the distance to a subspace ................. 379
12.7 Fitting functions to data: least squares
approximation ......................................... 380
12.8 Learning outcomes ..................................... 383
12.9 Comments on activities ................................ 384
12.10 Exercises ............................................ 385
12.11 Problems ............................................. 386
13 Complex matrices and vector spaces ......................... 389
13.1 Complex numbers ....................................... 389
13.2 Complex vector spaces ................................. 398
13.3 Complex matrices ...................................... 399
13.4 Complex inner product spaces .......................... 401
13.5 Hermitian conjugates .................................. 407
13.6 Unitary diagonalisation and normal matrices ........... 412
13.7 Spectral decomposition ................................ 415
13.8 Learning outcomes ..................................... 420
13.9 Comments on activities ................................ 421
13.10 Exercises ............................................ 424
13.11 Problems ............................................. 426
Comments on exercises ...................................... 431
Index ......................................................... 513 n ............................. 191
6.6 Learning outcomes ..................................... 199
6.7 Comments on activities ................................ 199
6.8 Exercises ............................................. 202
6.9 Problems .............................................. 205
7 Linear transformations and change of basis ................. 210
7.1 Linear transformations ................................ 210
7.2 Range and null space .................................. 220
7.3 Coordinate change ..................................... 223
7.4 Change of basis and similarity ........................ 229
7.5 Learning outcomes ..................................... 235
7.6 Comments on activities ................................ 235
7.7 Exercises ............................................. 239
7.8 Problems .............................................. 242
8 Diagonalisation ............................................ 247
8.1 Eigenvalues and eigenvectors .......................... 247
8.2 Diagonalisation of a square matrix .................... 256
8.3 When is diagonalisation possible? ..................... 263
8.4 Learning outcomes ..................................... 272
8.5 Comments on activities ................................ 273
8.6 Exercises ............................................. 274
8.7 Problems .............................................. 276
9 Applications of diagonalisation ............................ 279
9.1 Powers of matrices .................................... 279
9.2 Systems of difference equations ....................... 282
9.3 Linear systems of differential equations .............. 296
9.4 Learning outcomes ..................................... 303
9.5 Comments on activities ................................ 303
9.6 Exercises ............................................. 305
9.7 Problems .............................................. 308
10 Inner products and orthogonality ........................... 312
10.1 Inner products ........................................ 312
10.2 Orthogonality ......................................... 316
10.3 Orthogonal matrices ................................... 319
10.4 Gram-Schmidt orthonormalisation process ............... 321
10.5 Learning outcomes ..................................... 323
10.6 Comments on activities ................................ 324
10.7 Exercises ............................................. 325
10.8 Problems .............................................. 326
11 Orthogonal diagonalisation and its applications ............ 329
11.1 Orthogonal diagonalisation of symmetric matrices ...... 329
11.2 Quadratic forms ....................................... 339
11.3 Learning outcomes ..................................... 355
11.4 Comments on activities ................................ 356
11.5 Exercises ............................................. 358
11.6 Problems .............................................. 360
12 Direct sums and projections ................................ 364
12.1 The direct sum of two subspaces ....................... 364
12.2 Orthogonal complements ................................ 367
12.3 Projections ........................................... 372
12.4 Characterising projections and orthogonal
projections ........................................... 374
12.5 Orthogonal projection onto the range of a matrix ...... 376
12.6 Minimising the distance to a subspace ................. 379
12.7 Fitting functions to data: least squares
approximation ......................................... 380
12.8 Learning outcomes ..................................... 383
12.9 Comments on activities ................................ 384
12.10 Exercises ............................................ 385
12.11 Problems ............................................. 386
13 Complex matrices and vector spaces ......................... 389
13.1 Complex numbers ....................................... 389
13.2 Complex vector spaces ................................. 398
13.3 Complex matrices ...................................... 399
13.4 Complex inner product spaces .......................... 401
13.5 Hermitian conjugates .................................. 407
13.6 Unitary diagonalisation and normal matrices ........... 412
13.7 Spectral decomposition ................................ 415
13.8 Learning outcomes ..................................... 420
13.9 Comments on activities ................................ 421
13.10 Exercises ............................................ 424
13.11 Problems ............................................. 426
Comments on exercises ...................................... 431
Index ......................................................... 513
|