Commonly used notation ......................................... ix
Preface ........................................................ xi
1 Introduction ................................................. 1
2 Examples ..................................................... 8
2.1 Data example on S1: wind and ozone ...................... 8
2.2 Data examples on S2: paleomagnetism ..................... 8
2.3 Data example on ∑2k shapes of gorilla skulls ........... 12
2.4 Data example on ∑2k: brain scan shapes of
schizophrenic and normal patients ...................... 15
2.5 Data example on affine shape space A∑2k: application
to handwritten digit recognition ....................... 17
2.6 Data example on reflection similarity shape space R∑3k
glaucoma detection ..................................... 18
2.7 References ............................................. 20
3 Location and spread on metric spaces ........................ 21
3.1 Introduction ........................................... 21
3.2 Location on metric spaces .............................. 22
3.3 Variation on metric spaces ............................. 27
3.4 Asymptotic distribution of the sample mean ............. 28
3.5 Asymptotic distribution of the sample variation ........ 30
3.6 An example: the unit circle ............................ 31
3.7 Data example on S1 ..................................... 34
3.8 References ............................................. 35
4 Extrinsic analysis on manifolds ............................. 36
4.1 Extrinsic mean and variation ........................... 36
4.2 Asymptotic distribution of the sample extrinsic mean ... 37
4.3 Asymptotic distribution of the sample extrinsic
variation .............................................. 39
4.4 Asymptotic joint distribution of the sample extrinsic
mean and variation ..................................... 41
4.5 Two-sample extrinsic tests ............................. 42
4.6 Hypothesis testing using extrinsic mean and variation .. 46
4.7 Equivariant embedding .................................. 48
4.8 Extrinsic analysis on the unit sphere Sd ............... 49
4.9 Applications on the sphere ............................. 51
4.10 References ............................................. 55
5 Intrinsic analysis on manifolds ............................. 57
5.1 Intrinsic mean and variation ........................... 57
5.2 Asymptotic distribution of the sample intrinsic mean ... 59
5.3 Intrinsic analysis on Sd ............................... 64
5.4 Two-sample intrinsic tests ............................. 65
5.5 Data example on S2 ..................................... 69
5.6 Some remarks ........................................... 71
5.7 References ............................................. 75
6 Landmark-based shape spaces ................................. 77
6.1 Introduction ........................................... 77
6.2 Geometry of shape manifolds ............................ 78
6.3 References ............................................. 80
7 Kendall's similarity shape spaces ∑mk ....................... 82
7.1 Introduction ........................................... 82
7.2 Geometry of similarity shape spaces .................... 83
7.3 References ............................................. 86
8 The planar shape space ∑2k .................................. 87
8.1 Introduction ........................................... 87
8.2 Geometry of the planar shape space ..................... 88
8.3 Examples ............................................... 89
8.4 Intrinsic analysis on the planar shape space ........... 90
8.5 Other Fréchet functions ................................ 96
8.6 Extrinsic analysis on the planar shape space ........... 97
8.7 Extrinsic mean and variation ........................... 98
8.8 Asymptotic distribution of the sample extrinsic mean ... 99
8.9 Two-sample extrinsic tests on the planar shape space .. 101
8.10 Planar size-and-shape manifold ........................ 103
8.11 Applications .......................................... 105
8.12 References ............................................ 109
9 Reflection similarity shape spaces R∑mk .................... 110
9.1 Introduction .......................................... 110
9.2 Extrinsic analysis on the reflection shape space ...... 111
9.3 Asymptotic distribution of the sample extrinsic mean .. 117
9.4 Two-sample tests on the reflection shape spaces ....... 122
9.5 Other distances on the reflection shape spaces ........ 123
9.6 Application: glaucoma detection ....................... 125
9.7 References ............................................ 128
10 Stiefel manifolds VKm ...................................... 130
10.1 Introduction .......................................... 130
10.2 Extrinsic analysis on Vk,m ............................ 130
10.3 References ............................................ 134
11 Affine shape spaces A∑mk ................................... 135
11.1 Introduction .......................................... 135
11.2 Geometry of affine shape spaces ....................... 137
11.3 Extrinsic analysis on affine shape spaces ............. 139
11.4 Asymptotic distribution of the sample extrinsic mean .. 141
11.5 Application to handwritten digit recognition .......... 144
11.6 References ............................................ 146
12 Real projective spaces and projective shape spaces ......... 147
12.1 Introduction .......................................... 147
12.2 Geometry of the real projective space 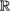 Pm ............. 148
12.3 Geometry of the projective shape space P0∑mk .......... 149
12.4 Intrinsic analysis on Pm ............. 148
12.3 Geometry of the projective shape space P0∑mk .......... 149
12.4 Intrinsic analysis on 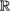 Pm ............................. 150
12.5 Extrinsic analysis on Pm ............................. 150
12.5 Extrinsic analysis on 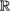 Pm ............................. 151
12.6 Asymptotic distribution of the sample extrinsic mean .. 153
12.7 References ............................................ 155
13 Nonparametric Bayes inference on manifolds ................. 156
13.1 Introduction .......................................... 156
13.2 Density estimation on metric spaces ................... 157
13.3 Full support and posterior consistency ................ 158
13.4 Posterior computations ................................ 163
13.5 Application to unit sphere Sd ......................... 165
13.6 Application to the planar shape space ∑2k ............. 166
13.7 Application to morphometries: classification of
gorilla skulls ........................................ 168
13.8 Proofs of theorems .................................... 170
13.9 References ............................................ 181
14 Nonparametric Bayes regression, classification and
hypothesis testing on manifolds ............................ 182
14.1 Introduction .......................................... 182
14.2 Regression using mixtures of product kernels .......... 183
14.3 Classification ........................................ 185
14.4 Nonparametric Bayes testing ........................... 192
14.5 Examples .............................................. 196
14.6 Proofs ................................................ 202
Appendix A Differentiable manifolds ....................... 209
Appendix В Riemannian manifolds ........................... 214
Appendix С Dirichlet processes ............................ 218
Appendix D Parametric models on Sd and ∑2k ................ 225
References .................................................... 229
Index ......................................................... 235 Pm ............................. 151
12.6 Asymptotic distribution of the sample extrinsic mean .. 153
12.7 References ............................................ 155
13 Nonparametric Bayes inference on manifolds ................. 156
13.1 Introduction .......................................... 156
13.2 Density estimation on metric spaces ................... 157
13.3 Full support and posterior consistency ................ 158
13.4 Posterior computations ................................ 163
13.5 Application to unit sphere Sd ......................... 165
13.6 Application to the planar shape space ∑2k ............. 166
13.7 Application to morphometries: classification of
gorilla skulls ........................................ 168
13.8 Proofs of theorems .................................... 170
13.9 References ............................................ 181
14 Nonparametric Bayes regression, classification and
hypothesis testing on manifolds ............................ 182
14.1 Introduction .......................................... 182
14.2 Regression using mixtures of product kernels .......... 183
14.3 Classification ........................................ 185
14.4 Nonparametric Bayes testing ........................... 192
14.5 Examples .............................................. 196
14.6 Proofs ................................................ 202
Appendix A Differentiable manifolds ....................... 209
Appendix В Riemannian manifolds ........................... 214
Appendix С Dirichlet processes ............................ 218
Appendix D Parametric models on Sd and ∑2k ................ 225
References .................................................... 229
Index ......................................................... 235
|